#|message: false
#|warning: false
pacman::p_load(car,
dplyr,
flextable,
ggplot2,
ggpubr,
ggsci,
knitr,
lmtest,
readxl,
rstatix)17 Correlação
17.1 Pacotes usados neste capítulo
17.2 Introdução
A correlação é usada para avaliar a força e a direção da relação entre duas variáveis numéricas contínuas, normalmente distribuídas. A maneira mais comum de mostrar a relação entre duas variáveis quantitativas é através de um diagrama ou gráfico de dispersão (scatterplot). A Figura 17.1 exibe um exemplo de um gráfico de dispersão, onde se observa um padrão geral que sugere uma relação entre o estriol urinário (mg/24h) e o peso fetal em uma gravidez normal (Greene Jr e Touchstone 1963).

O gráfico de dispersão mostra que os valores de uma variável aparecem no eixo horizontal x e os valores da outra variável aparecem no eixo vertical y. Cada indivíduo nos dados aparece como o ponto no gráfico fixado pelos valores de ambas as variáveis para aquele indivíduo. Normalmente, eixo x é a variável explicativa (ou variável explanatória ou independente) e y a variável desfecho (variável resposta ou dependente).
Em um diagrama de dispersão deve-se procurar o padrão geral e desvios marcantes desse padrão. Verifica-se o padrão geral, observando a direção, a forma e força do relacionamento. Um tipo importante de desvio é um valor atípico, um valor individual que está fora do padrão geral do relacionamento.
A Figura 17.1 mostra uma clara direção do padrão geral que se move da esquerda inferior para a direita superior. Este comportamento é denominado de correlação positiva entre as variáveis. A forma do relacionamento é aproximadamente uma linha reta com uma ligeira curva para a direita à medida que se move para cima. A força de uma correlação em um gráfico de dispersão é determinada pela proximidade dos pontos em uma forma clara. No caso, quanto mais se aproxima de uma reta, mais forte é a associação, no caso de uma correlação linear. Duas variáveis estão negativamente associadas quando se comportam de forma oposta ao da Figura 17.1.
Obviamente, nem todos os diagramas de dispersão mostram uma direção clara que permita descrever como correlação positiva ou negativa e não tem uma forma linear, sugerindo que não há correlação, como a Figura 17.2.

17.3 Coeficiente de correlação de Pearson
A correlação é quantificada pelo Coeficiente de Correlação Linear de Pearson. Este coeficiente paramétrico, denotado por r, é um número adimensional, independente das unidades usadas para medir as variáveis x e y.
Suponha que se tenha dados sobre as variáveis x e y para n indivíduos. Os valores para o primeiro indivíduo são \({x}_{1}\) e \({y}_{1}\), os valores para o segundo indivíduo são \({x}_{2}\) e \({y}_{2}\) e assim por diante. As médias e desvios padrão das duas variáveis são \(\bar{x}\) e \({s}_{x}\) para os valores de x e \(\bar{y}\) e \({s}_{y}\) para os valores de y. A correlação r entre x e y é dada pela equação:
\[ r = \frac{\sum{(x_{1} - \bar{x})(y_{1} - \bar{y})}}{{\sqrt{\sum (x_{1} - \bar{x})^2\times\sum (y_{1} - \bar{y})^2}}} \]
O Coeficiente de Correlação, r, apresenta as seguintes características:
É um valor numérico que varia de -1 a +1 (Figura 17.3):
- Quando r = -1, há uma correlação linear negativa ou inversa perfeita;
- Quando r = +1, há uma correlação linear positiva ou direta perfeita;
- Quando r = 0, não há correlação entre as variáveis.

Quanto mais os pontos se aproximam de uma linha reta, maior a magnitude de r.
O coeficiente de correlação r é calculado para uma amostra e é uma estimativa do coeficiente de correlação da população \(\rho\) (leia-se rô).
A correlação não faz distinção entre variáveis explicativas e variáveis resposta. Apesar de haver uma recomendação para que x seja a variável explanatória e y a variável desfecho. Não faz diferença qual variável será chamada chama de x e qual de y no cálculo da correlação.
Como r usa os valores padronizados das observações, r não muda se as unidades de medida de x, y ou ambos são modificados. A correlação r em si não tem unidade de medida; é apenas um número.
17.4 Dados usados no exemplo
Está bem definido que existe uma relação entre a idade de crianças e a sua altura (comprimento). Os dados de 40 crianças com idade entre 18 e 36 meses (20 meninos e 20 meninas) foram coletados em um ambulatório pediátrico. A idade foi registrada em meses e o comprimento em centímetros.
Os dados estão no banco de dadosdadosReg.xlsx que pode ser obtido aqui. Baixe e salve o arquivo no seu diretório de trabalho.
17.4.1 Leitura e exploração dos dados
A função read_excel do pacote readxl será usada para carregar o arquivo. Observar os dados com a função str().
dados <- read_excel("dados/dadosReg.xlsx")
str(dados)tibble [40 × 5] (S3: tbl_df/tbl/data.frame)
$ id : num [1:40] 1 2 3 4 5 6 7 8 9 10 ...
$ idade : num [1:40] 18 18 19 19 20 20 21 21 22 22 ...
$ comp : num [1:40] 80 80 83 82 84 81 84.5 84 85 82.5 ...
$ irmaos: num [1:40] 0 0 2 0 0 1 1 1 0 1 ...
$ sexo : chr [1:40] "masc" "fem" "masc" "fem" ...De acordo com uma das exigências da correlação, as variáveis idade e comp pertencem a classe das variáveis numéricas. A variável sexo foi lida como um variável numérica e será transformada em fator:
dados$sexo <- as.factor(dados$sexo)Após esta pequena manipulação, será feita a sumarização dos dados.
17.4.2 Sumarização e visualização dos dados
Esta ação será realizada com a função get_summary_stats () do pacote rstatix que necessita dos seguintes argumentos:
dados %>%
rstatix::get_summary_stats(idade,
comp,
type = "mean_sd")# A tibble: 2 × 4
variable n mean sd
<fct> <dbl> <dbl> <dbl>
1 idade 40 27.0 5.41
2 comp 40 90.2 6.00Para visualizar os dados, será usado o gráfico de dispersão (Figura 17.4), usando a função geom_point() do pacote ggplot2:
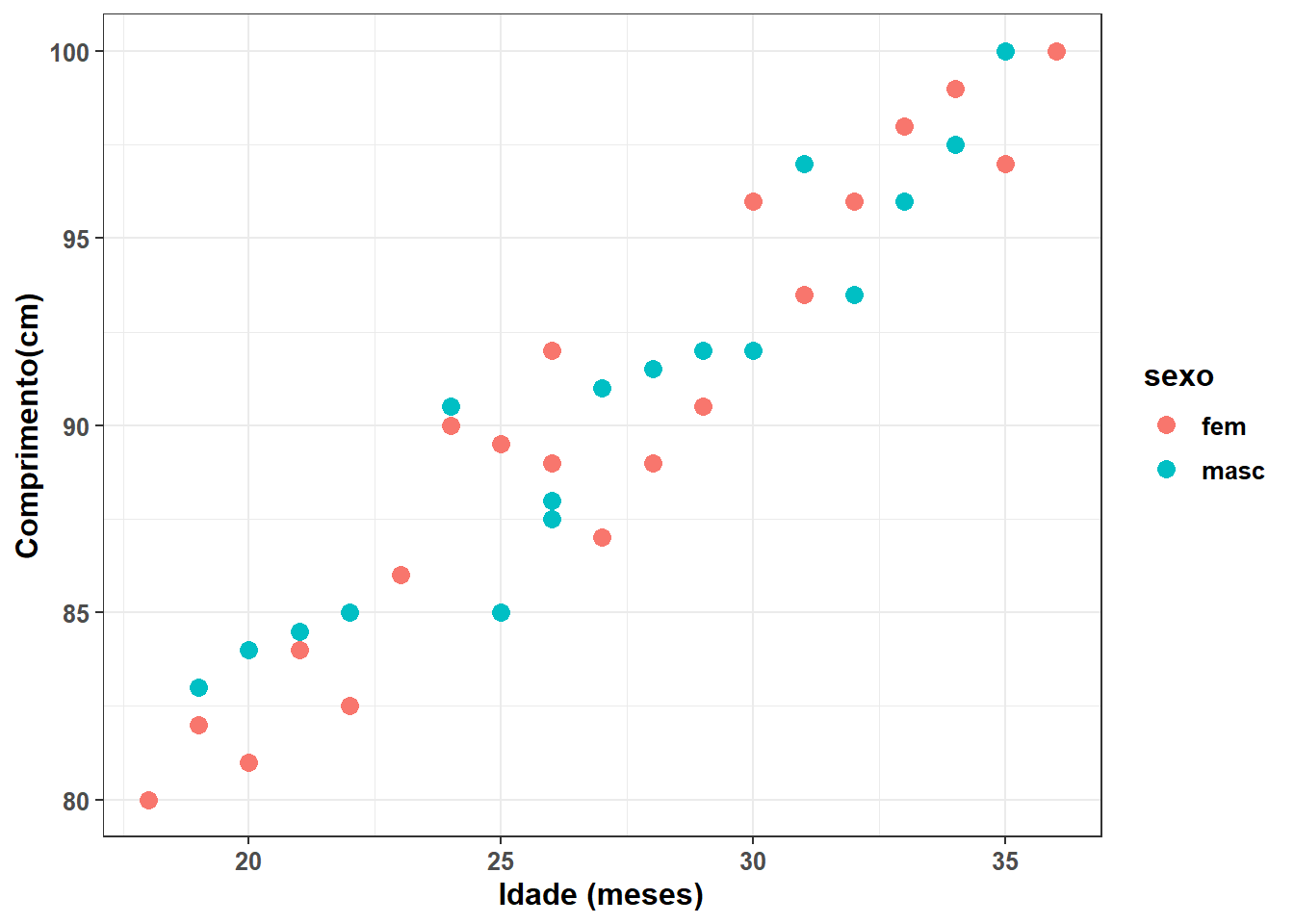
A separação dos pontos por sexo, usando cores diferentes, não muda a análise e foi realizada apenas para treinamento (e curiosidade!), pois não há motivo para que haja diferença na correlação entre os sexos.
17.5 Pressupostos da correlação
A primeira e mais importante etapa antes de analisar os dados, usando a correlação de Pearson, é verificar se é apropriado usar este teste estatístico.
Serão discutidos sete pressupostos, três estão relacionados com o projeto do estudo e como as variáveis foram medidas (pressupostos 1, 2 e 3) e quatro que se relacionam com as características dos dados (pressupostos 4, 5, 6 e 7) (Kassambara 2021).
- Variáveis numéricas contínuas
As duas variáveis devem ser medidas em uma escala contínua (são medidas no nível intervalar ou de razão). No exemplo, tanto a variável idade como o comprimento (comp) são variáveis contínuas.
- Variáveis devem estar como pares
As duas variáveis contínuas devem ser emparelhadas, o que significa que cada caso (por exemplo, cada participante) tem dois valores: um para cada variável.
- Independência das observações
Deve haver independência de casos, o que significa que as duas observações para um caso (por exemplo, a idade e o comprimento) devem ser independentes das duas observações para qualquer outro caso.
Se estes pressupostos forem atendidos, avalia-se os outros pressupostos:
- Relação linear entre as variáveis
O coeficiente de correlação de Pearson é uma medida da força de uma associação linear entre duas variáveis. Dito de outra forma, ele determina se há um componente linear de associação entre duas variáveis contínuas. Por esse motivo, verifica-se a relação entre duas variáveis, em um gráfico de dispersão, para ver se a execução de uma correlação de Pearson é a melhor escolha como medida de associação.
A variável idade é colocada como variável preditora (eixo x) e comp como desfecho (eixo y). O gráfico de dispersão anterior, mostra uma nítida correlação linear.
- Normalidade das variáveis
Para verificar se as variáveis têm distribuição normal, é possível usar o teste de Shapiro-Wilk, usando a função shapiro_test(), incluída no pacote rstatix:
dados %>% shapiro_test(idade, comp)# A tibble: 2 × 3
variable statistic p
<chr> <dbl> <dbl>
1 comp 0.958 0.141
2 idade 0.958 0.145O teste de Shapiro-Wilk de ambas as variáveis retorna um valorp> 0,05, indicando que não é possível rejeitar a \(H_{0}\); os dados seguem a distribuição normal, portanto o pressuposto foi atendido.
- Pesquisa de valores atípicos
A identificação dos valores atípicos pode ser feita usando a função identify_outliers() do pacote rstatix.
dados %>% identify_outliers(idade)[1] id idade comp irmaos sexo is.outlier is.extreme
<0 linhas> (ou row.names de comprimento 0) dados %>% identify_outliers(comp)[1] id idade comp irmaos sexo is.outlier is.extreme
<0 linhas> (ou row.names de comprimento 0)- Homoscedasticidade
A homocedasticidade assume que os dados são igualmente distribuídos sobre a linha de regressão. Descreve uma situação na qual o resíduo é o mesmo em todos os valores das variáveis independentes. A heterocedasticidade (a violação da homocedasticidade) está presente quando o tamanho dos resíduos difere entre os valores de uma variável independente.
O impacto de violar o pressuposto da homocedasticidade é uma questão de grau, aumentando à medida que a heterocedasticidade aumenta. Dessa forma, avalia-se a homocedasticidade, observando os resíduos.
Uma correlação linear pode ser descrita por uma reta. Em uma correlação linear perfeita, a reta passa por todos os pontos. Normalmente, não é possível traçar uma reta que passe por todos os pontos. A melhor reta é aquela que promove o melhor ajuste,ou seja, é aquela cuja distância dos pontos até a reta é a menor possível. Os resíduos são a diferença entre o valor observado e o valor previsto pelo melhor ajuste, estabelecido pelo modelo de regressao linear.
- Construção do modelo: Para ajustar a um modelo linear, usa-se a função
lmque deve conter um objeto da classeformulatipo (x ~ y) como argumento. Demais características da função podem ser obtidas com?lmou direto na ajuda doRStudio. O modelo será atribuído a um objeto denominadomod_reg.
mod_reg <- lm(comp ~ idade, dados)- Análise gráfica da homoscedasticidade: Pode ser feita através dos gráficos diagnósticos para a regressão linear, utilizados para verificar se o modelo funciona bem para representar os dados. Uma forma de avaliar é verificar como as variâncias se comportam. Os gráficos diagnósticos são apresentados de quatro maneiras diferentes.1 Neste estágio, serão avaliados o primeiro e o terceiro tipo (Figura 17.5).
par(mfrow=c(1,2)) # muda o layout do painel para 1 linha e 2 colunas
plot(mod_reg, which=c(1,3))
par(mfrow=c(1,1)) # retorna o layaout do painel para o padrão de 1 linha e 1 coluna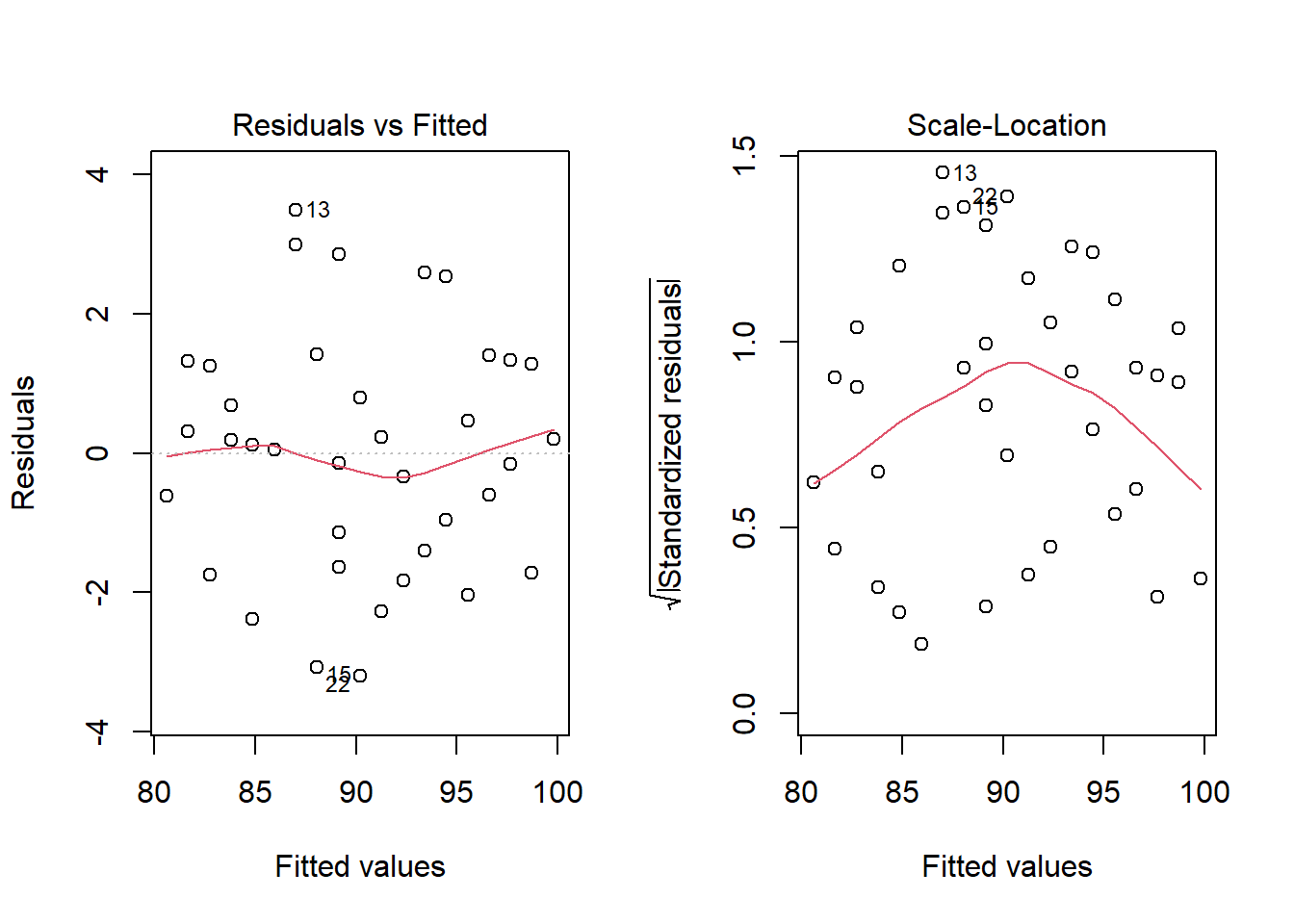
No gráfico 1, tem-se os resíduos em função dos valores estimados. Pode-se utilizar este gráfico para observar a independência e a homocedasticidade, se os resíduos se distribuem de maneira razoavelmente aleatória e com mesma amplitude em torno do zero.
No gráfico 3 (valores ajustados x resíduos), tem-se os resíduos em função dos valores estimados. Pode-se utilizar este gráfico para observar a independência e a homocedasticidade, se os resíduos se distribuem de maneira razoavelmente aleatória e com mesma amplitude em torno do zero. Permite verificar se há outliers - valores de resíduos padronizados acima de 3 ou abaixo de -3. Embora o gráfico possa dar uma ideia sobre homocedasticidade, às vezes, um teste mais formal é preferido. Existem vários testes para isso, mas aqui será utilizado o Teste de Breusch-Pagan (Halunga, Orme, e Yamagata 2017). A \(H_{0}\) e a \(H_{1}\) podem ser consideradas como:
\(H_{0}\): Homocedasticidade. Os resíduos têm variância constante sobre o modelo verdadeiro.
\(H_{1}\): Heterocedasticidade. Os resíduos não têm variância constante sobre o modelo verdadeiro.
Se o valor p > 0,05 não se rejeita a \(H_{0}\) de homocedasticidade. O teste de Breusch-Pagan é encontrado na função bptest(), incluída no pacote lmtest:
lmtest::bptest(mod_reg)
studentized Breusch-Pagan test
data: mod_reg
BP = 0.049988, df = 1, p-value = 0.8231Os resultados não indicam heteroscedasticidade e isso é bom. Desta forma, pode-se aplicar a equação final de predição.
17.6 Execução do teste de correlação
17.6.1 Coeficiente de correlação de Pearson (r)
O coeficiente de correlação, r, é calculado para uma amostra e é uma estimativa do coeficiente de correlação da população \(\rho\) (rô).
Como visto, no início deste capítulo, a correlação não faz distinção entre variáveis explicativas e variáveis resposta. Apesar de haver uma recomendação para que x seja a variável explanatória e y a variável desfecho. Não faz diferença qual variável será chamada chama de x e qual de y no cálculo da correlação.
Como o r usa os valores padronizados das observações, não muda nada se as unidades de medida de x, y ou ambas são modificadas. A correlação r em si não tem unidade de medida; é apenas um número.
O cálculo pode ser realizado com a função cor_test() do pacote rstatix que usa os seguintes argumentos:
- data \(\to\) dataframe contendo as variáveis;
- … \(\to\) Uma ou mais expressões (ou nomes de variáveis) sem aspas separadas por vírgulas. Usado para selecionar uma variável de interesse. Alternativa ao argumento
vars. Ignorado quandovarsé especificado; - vars2 \(\to\) • vetor de caracteres opcional. Se especificado, cada elemento em vars será testado em relação a todos os elementos em vars2. Aceita nomes de variáveis sem aspas: c(var1, var2);
- alternative \(\to\) hipótese alternativa “two.sided” (bilateral) ou “greater” ou “less” (unilateral a direita ou a esquerda, respectivamente);
- method \(\to\) ⟶ qual coeficiente de correlação deve ser usado para o teste. Um dos termos “pearson”, “kendall” ou “spearman” pode ser abreviado;
- conf.level \(\to\) nivel de confiança. Padrão 0.95.
r <- dados %>% cor_test(idade,
comp,
method = "pearson")
r# A tibble: 1 × 8
var1 var2 cor statistic p conf.low conf.high method
<chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <chr>
1 idade comp 0.96 21.4 7.87e-23 0.927 0.979 PearsonA saída do Coeficiente de Correlação de Pearson (r) é igual 0.96 (IC95%: 0.93, 0.98) o que corresponde a uma correlação linear muito forte (Tabela 17.1)) entre a idade e o comprimento de crianças (Schober, Boer, e Schwarte 2018).
O coeficiente refere a existência de correlação linear, mas não especifica se a relação é de causa e efeito. O valorpespecifica se a correlação é igual a zero (\(H_{0}\)) ou diferente de zero (\(H_{1}\)). No caso, ela é diferente de zero.
O importante é a magnitude do r, entretanto, o coeficiente r e o valorpdevem ser interpretados em conjunto. Se o valorp> 0,05, mesmo que r seja diferente de zero, a correlação não deveria ser interpretada.
Coeficiente de Correlação (r) | Interpretação |
|---|---|
0,0<0,3 | desprezável |
0,3<0,5 | fraca |
0,5,0,7 | moderada |
0,7<0,9 | forte |
0,9<1,0 | muito forte |
1,0 | perfeita |
Talvez a melhor maneira de interpretar a correlação linear é elevar o valor do r ao quadrado para obter o Coeficiente de Determinação (\(R^{2}\)). No exemplo usado, tem-se que o \(R^{2}\) é igual a \(0,96^{2} = 0,922\), então, 92,2% da variação do comprimento da criança (y) podem ser explicados, nesses dados, pela variação da sua idade (x), fato mais ou menos óbvio!.
17.6.2 Coeficiente de correlação de Spearman (\(\rho\))
Se os pressupostos são violados é recomendado o uso de correlação não paramétrica (veja a Seção 20.2), incluindo testes de correlação baseados em postos (veja a Seção 20.3) de Spearman e Kendall (De Winter, Gosling, e Potter 2016).
Para calcular o coeficente, Usar a mesma função da correlação de Pearson, mudando o argumento method:
rho <- dados %>% cor_test(idade,
comp,
method = "spearman")
rho# A tibble: 1 × 6
var1 var2 cor statistic p method
<chr> <chr> <dbl> <dbl> <dbl> <chr>
1 idade comp 0.96 448. 3.30e-22 Spearman17.6.3 Coeficiente de correlação de Kendall (\(\tau\))
O coeficiente de correlação de postos de Kendall ou estatística tau de Kendall é usado para estimar uma medida de associação baseada em postos. Pode ser usado com variáveis ordinais ou quando não existe relação linear entre as variáveis. Uma vantagem sobre o coeficiente de Spearman é a possibilidade de ser generalizado para um coeficiente de correlação parcial. Deve ser usada ao invés do coeficiente de Spearman quando se tem um conjunto pequeno de dados com um grande número de postos empatados (veja a Seção 20.3). Para o cálculo desse coeficiente, continua-se com a mesma função anterior, mudando o method = “kendall”.
tau <- dados %>% cor_test(idade,
comp,
method = "kendall")
tau# A tibble: 1 × 6
var1 var2 cor statistic p method
<chr> <chr> <dbl> <dbl> <dbl> <chr>
1 idade comp 0.85 7.57 3.64e-14 KendallNo caso normal, a correlação de Kendall é mais robusta e eficiente que a correlação de Spearman. Isso significa que a correlação de Kendall é preferida quando há amostras pequenas ou alguns valores atípicos. O rho de Spearman geralmente é maior que o tau de Kendall.
Maiores detalhes sobre os testes diagnósticos podem ser encontrados em: https://data.library.virginia.edu/diagnostic-plots/↩︎