Capítulo 17 Métodos não paramétricos

17.1 Pacotes necessários neste capítulo

pacman::p_load (coin,
                confintr,
                dplyr,
                ggplot2,
                ggpubr,
                ggsci,
                kableExtra,
                knitr,
                readxl,
                rstatix,
                tidyr)

17.2 Distribuição livre

A maioria dos testes estatísticos que discutidos são testes paramétricos. Nestes, o interesse estava focado em estimar ou testar uma hipótese sobre um ou mais parâmetros populacionais. Além disso, o aspecto central desses procedimentos era o conhecimento da forma funcional da população da qual foram retiradas as amostras que forneceram a base para a inferência. Por exemplo, o teste t de Student para amostras independentes e a ANOVA são baseados no pressuposto de que os dados foram amostrados de populações que têm distribuição normal.

Os testes não paramétricos não fazem suposições em relação à distribuição da população. Não têm, portanto, os pressupostos restritivos, comuns nos testes paramétricos. Têm distribuição livre. São baseados em uma ideia simples de ordenação por postos, do valor mais baixo ao mais alto. Analisam somente os postos, ignorando os valores. Podem ser usados tanto com variáveis ordinais como quantitativas numéricas.

17.3 Postos

Os métodos estatísticos não paramétricos não lidam diretamente com os valores observados. Em função disso, para poder usar a informação fornecida pelas observações, sem trabalhar diretamente com os valores observados, utiliza-se os postos das observações. Posto (rank) de uma observação é a sua posição em relação aos demais valores.

A atribuição dos postos de uma variável é realizada da seguinte maneira:

Colocam-se as observações em ordem crescente;
Associam-se valores, correspondendo às suas posições relativas na amostra. O primeiro elemento recebe o valor 1, o segundo o valor 2 e, assim por diante, até que a maior observação receba o valor n;
Se todas as observações são distintas, os postos são iguais aos valores associados às observações no passo anterior.
Para observações iguais (empates), associam-se postos iguais à média das suas posições relativas na amostra.

Por exemplo, suponha uma amostra contendo os escores de Apgar no primeiro minuto de 10 recém-nascidos a termo (Tabela 17.1). Em primeiro lugar, os valores são colocados em ordem crescente e, após, atribui-se postos aos valores. Observe que os postos atribuídos aos valores das posições 3 e 4 são iguais e correspondentes a média de 3 e 4, que é igual a 3,5. O mesmo ocorreu com os outros valores onde houve empate. A soma dos postos, no exemplo, é igual a 55. Para verificar a correção do cálculo, haja ou não empates, a soma dos postos será sempre \(\frac {n\ \times \ (n+1)}{2}\). No exemplo, n = 10, logo \(\frac {10\ \times \ (10+1)}{2}=55\).

Tabela17.1: Tabela17.2: Construção dos postos
Apgar 1	Ordem	Posto
4	1	1.0
5	2	2.0
7	3	3.0
8	4	5.0
8	5	5.0
8	6	5.0
9	7	7.5
9	8	7.5
10	9	9.5
10	10	9.5

17.4 Teste de Mann-Whitney

O teste de Mann-Whitney é usado para analisar a diferença na variável dependente (desfecho) para dois grupos independentes. O teste classifica todos os valores dependentes, ou seja, o valor mais baixo obtém o posto um e, em seguida, usa a soma dos postos de cada grupo no cálculo da estatística de teste.

É o substituto do teste t para amostras independentes quando os pressupostos deste teste são violados. Para a aplicação do teste de Mann-Whitney a variável de interesse deve ser ordinal ou numérica. Este teste é equivalente ao desenvolvido por Frank Wilcoxon (1892 – 1965), assim algumas vezes é denominado de Wilcoxon Rank Sum Test. O R usa esta denominação e é importante não confundir com o teste não paramétrico para amostra pareadas, discutido mais adiante.

17.4.1 Dados usados nesta seção

O arquivo dadosCirurgia.xlsx, já usado na Seção 16.2.5.1, fornecerá os dados para esta seção. Ele contém 144 recém-nascidos que foram submetidos a diferentes procedimentos cirúrgicos. A questão de pesquisa a ser respondida é:

Existe diferença no tempo de hospitalização (tempohosp) dos recém-nascidos de acordo com a presença ou não de infecção (infec)?

Essa pergunta foi respondida de outra maneira, na Seção 16.2.5. Agora, será usado o teste de Mann-Whitney.

17.4.1.1 Leitura, exploração e visualização dos dados

Os dados serão lidos com a função read_excel() do pacote readxl:

cirurgia <- readxl::read_excel ("Arquivos/dadosCirurgia.xlsx")
str(cirurgia)

## tibble [144 × 7] (S3: tbl_df/tbl/data.frame)
##  $ id       : num [1:144] 1 2 3 4 5 6 7 8 9 10 ...
##  $ sexo     : chr [1:144] "masc" "masc" "masc" "masc" ...
##  $ peso     : num [1:144] 2020 1850 2540 1150 2900 ...
##  $ ig       : num [1:144] 36 30 38 31 36 37 38 39 38 39 ...
##  $ tempohosp: num [1:144] 37 37 37 46 37 36 30 18 25 14 ...
##  $ infec    : chr [1:144] "não" "não" "sim" "sim" ...
##  $ cirurgia : chr [1:144] "abdominal" "abdominal" "abdominal" "outra" ...

A variável infec aparece como caractere e será transformada como fator:

cirurgia$infec <- as.factor(cirurgia$infec)

Os boxplots (Figura 17.1), construídos com a função ggboxplot() do pacote ggpubr com as cores da paleta do New England Journal of Medicine (NEJM), são uma boa maneira de visualizar os dados:

ggpubr::ggboxplot(cirurgia,
                  x = "infec",
                  y = "tempohosp",
                  bxp.errorbar = TRUE,
                  bxp.errorbar.width = 0.1,
                  fill = "infec",
                  palette = "nejm",
                  legend = "none",
                  ggtheme = theme_bw(),
                  xlab = "Presença de infecção" ,
                  ylab = "Tempo de hospitalização (dias)")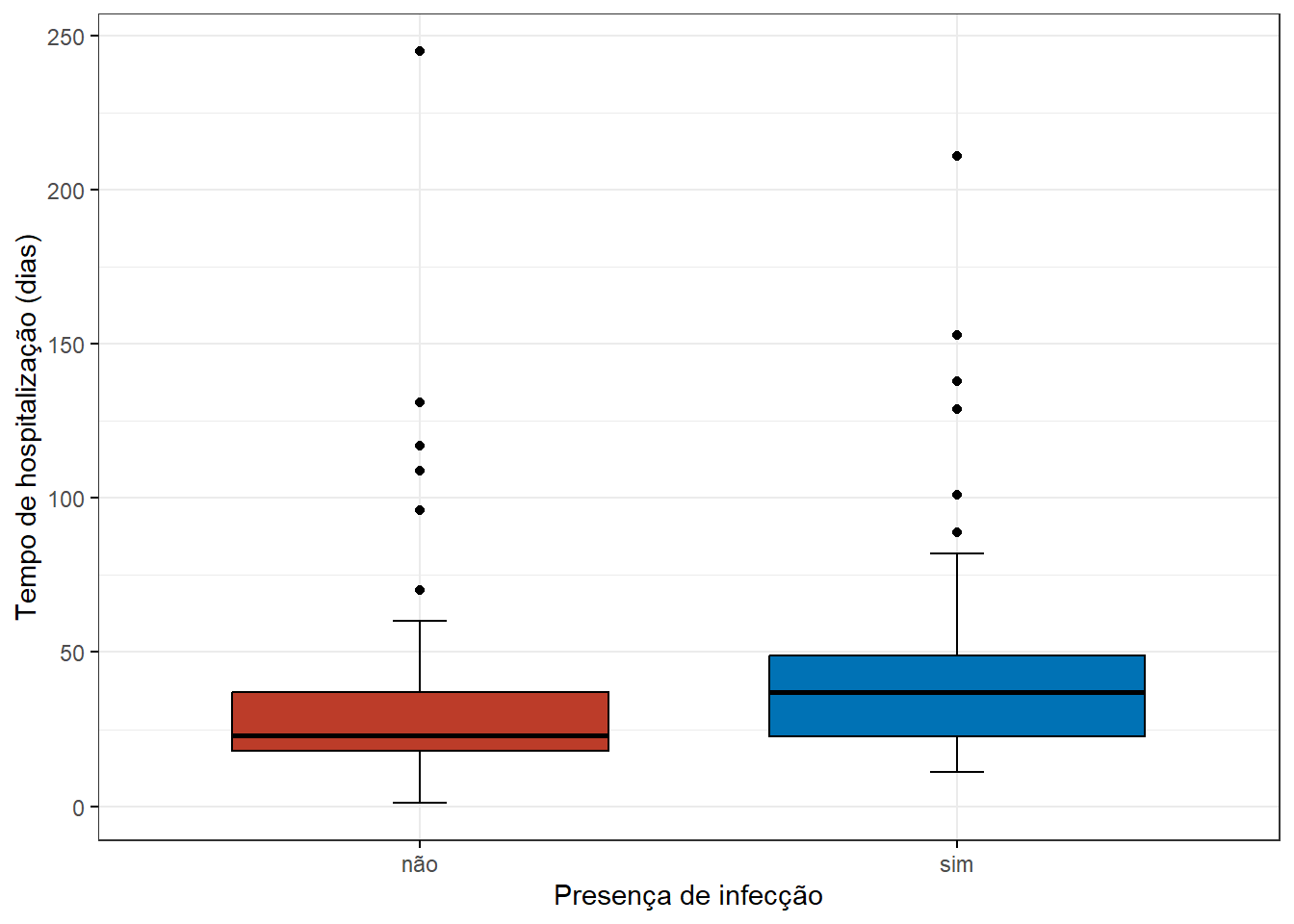

Figura17.1: Impacto da infecção no tempo de hopsitalização.

Os boxplots exibem uma série de valores atípicos, indicando que existe uma assimetria em ambos os grupos. Essa assimetria também pode ser verificada usando o teste de Shapiro-Wilk, que mostrando valores P < 0,05, confirma que os dados não seguem a distribuição normal. Este teste não é pré-requisito para o teste. Foi realizado como uma demonstração.

cirurgia %>% 
  dplyr::group_by(infec) %>% 
  rstatix::shapiro_test(tempohosp)

## # A tibble: 2 × 4
##   infec variable  statistic        p
##   <fct> <chr>         <dbl>    <dbl>
## 1 não   tempohosp     0.565 9.87e-15
## 2 sim   tempohosp     0.692 1.47e- 9

17.4.1.2 Sumarização dos dados

Como a variável tempohosp é assimétrica conforme mostrado acima, onde ambos os valores P são menores do que 0,05, será realizado um sumário numérico com a obtenção da mediana e IIQ. Isto será feito através da função group_by() e summarise(), incluídas no pacote dplyr.

resumo <- cirurgia %>% 
  dplyr::group_by(infec) %>% 
  dplyr::summarise(n = n(),
                   mediana = median (tempohosp, na.rm = TRUE),
                   p25=quantile(tempohosp, probs = 0.25, na.rm = TRUE),
                   p75=quantile(tempohosp, probs = 0.75, na.rm = TRUE))
resumo

## # A tibble: 2 × 5
##   infec     n mediana   p25   p75
##   <fct> <int>   <dbl> <dbl> <dbl>
## 1 não      88      23  18      37
## 2 sim      56      37  22.8    49

Os dados mostram que a mediana de tempo de internação dos neonatos infectados é bem maior do que os não infectados. A diferença mediana e os intervalos de confiança para essa diferença pode ser calculada com a função ci_quantile_diff() do pacote confintr (145).

infectado <- dplyr::filter(cirurgia, infec == "sim") %>% 
  select(tempohosp)
sem_infec <- dplyr::filter(cirurgia, infec == "não") %>% 
  select(tempohosp)

dif_mediana <- median(infectado$tempohosp)- median(sem_infec$tempohosp)
dif_mediana

## [1] 14

ci_quantile_diff(infectado, sem_infec)

## 
##  Two-sided 95% bootstrap confidence interval for the population value of
##  50% quantile(x) - 50% quantile(y) based on 9999 bootstrap replications
##  and the bca method
## 
## Sample estimate: 14 
## Confidence interval:
##  2.5% 97.5% 
##   4.5  19.5

Dessa forma, a mediana da diferença entre os dois grupos foi de 14 dias (IC95%; 5 - 20).

17.4.2 Hipóteses estatísticas

Da mesma maneira que o teste t, as hipóteses estabelecidas comparam dois grupos independentes. Se não houver diferença entre os grupos, ou seja, os grupos são provenientes de uma mesma população, as somas dos postos em cada grupo devem ficar próximas. Desta forma,

\(H_{0}\): As duas populações são iguais.
\(H_{1}\): As duas populações não são iguais.

Não foi escrita a hipótese nula como sendo de que as médias (ou as medianas) são iguais, pois o teste não usa as medidas de posição tradicionais e sim os postos.

17.4.3 Pressupostos do teste de Mann_Whitney

O teste de Mann-Whitney é baseado nos seguintes pressupostos:

Os dados são aleatórios;
As amostras são de dois grupos independentes;
Um dos grupos é denominado de 1 e o outro de 2;
A variável a ser comparada nos grupos deve ser ordenável;
O grupo 1 será o grupo de menor tamanho e, se tiverem o mesmo tamanho, o grupo 1 é aquele cuja soma dos postos é a menor.

17.4.4 Cálculo da estatística de teste

17.4.4.1 Lógica do teste U de Mann-Whitney

De acordo com as hipóteses estabelecidas, o teste é bicaudal. Se as observações nos dois grupos forem provenientes da mesma população, a soma dos postos em cada grupo devem ficar próximas.

Para calcular o teste, procede-se da seguinte maneira:

Deve haver uma variável que identifique o grupo a que pertence cada uma das observações. No exemplo proposto, a variável desfecho é tempohosp e a variável agrupadora é infec, categorizada como sim e não.
Ordenar de forma crescente todos os valores da variável tempohosp, sem levar em consideração a que grupo pertence. Para realizar este procedimento, será usada a função rank() do R base com o método para empates igual à média dos valores empatados (ties.method="average). Ao executar a função, será criada uma nova variável, denotada postos.

cirurgia$postos <- rank(cirurgia$tempohosp, ties.method = "average") 
head(cirurgia)

## # A tibble: 6 × 8
##      id sexo   peso    ig tempohosp infec cirurgia  postos
##   <dbl> <chr> <dbl> <dbl>     <dbl> <fct> <chr>      <dbl>
## 1     1 masc   2020    36        37 não   abdominal   94.5
## 2     2 masc   1850    30        37 não   abdominal   94.5
## 3     3 masc   2540    38        37 sim   abdominal   94.5
## 4     4 masc   1150    31        46 sim   outra      120  
## 5     5 masc   2900    36        37 não   abdominal   94.5
## 6     6 fem    2480    37        36 sim   abdominal   91

Verificar o tamanho (n) de cada grupo (presença ou não de infecção) e somar os postos em cada um dos grupos, usando a função group_by() junto com a função summarise(),

resumo <- cirurgia %>% 
  dplyr::group_by(infec) %>% 
  dplyr::summarise(n = n(),
                   soma = sum(postos))
resumo

## # A tibble: 2 × 3
##   infec     n  soma
##   <fct> <int> <dbl>
## 1 não      88 5564.
## 2 sim      56 4876.

Denominar de grupo_1 o grupo com menor soma:

grupo_1 <- min(resumo$soma)
grupo_1

## [1] 4875.5

Denotar o grupo_1 como T

T <- grupo_1

Consequentemente,

n1 <- 56
n2 <- 88

Calcular a estística do teste, usando a fórmula preconizada por Altman (146):

\[ U =n_{1} \times n_{2} \ +\left [\frac{n_{1} \times \left (n_{1} + 1 \right )}{2} \right ] - T \]

U <- (n1*n2 + ((n1*(n1 + 1))/2)) - T
U

## [1] 1648.5

Obs.: O U de Mann-Whitney aparece no teste de Wilcoxon como W, eles são iguais

Se \(n_{1}\), \(n_{2}\) \(\ge\) 10, a distribuição da estatística do teste pode ser aproximada por uma distribuição normal com média igual a

\[ \mu_{U} =\left [\frac{n_{S} \times \left (n_{L} + 1 \right )}{2} \right ] \]

onde \(n_{S}\) e \(n_{L}\), são, respectivamente, o grupo de menor e maior tamanho. No exemplo, \(n_{1}\) e \(n_{2}\).

m_U <- (n1*(n1+n2+1))/2
m_U

## [1] 4060

E desvio padrão igual a

\[ \sigma_{U}= \sqrt {\frac{n_{L}\times \sigma_{U}}{6}} \]

dp_U <- sqrt((n2*m_U)/6)
dp_U

## [1] 244.0219

Os resultados fornecem os dados para calcular a estatística \(Z_{U}\) com correção de continuidade e, a partir dela, calcular o valor P.

\[ Z_{U}= \frac{(T -0,5) - \mu_{U}}{\sigma_{U}} \]

Z_U <- ((T - 0.5) - m_U)/dp_U
round(Z_U, 2)

## [1] 3.34

Finalmente, calcula-se o valor P, usando a função pnorm(), multiplicada por 2, pois o teste é bicaudal.

P <- pnorm(Z_U, lower.tail = FALSE) * 2
round(P, 4)

## [1] 8e-04

Na prática, não há necessidade de fazer todos esses cálculos, pois o R calcula facilmente o teste. Os cálculos foram mostrados para melhorar o entendimento de como o teste de Mann-Whitney funciona.

17.4.4.2 Cálculo do U de Mann-Whitney no R

O teste pode ser realizado com a função wilcox_test() ⁵⁷ do pacote rstatix:

teste <- rstatix::wilcox_test(formula = tempohosp ~ infec, data = cirurgia)
teste

## # A tibble: 1 × 7
##   .y.       group1 group2    n1    n2 statistic       p
## * <chr>     <chr>  <chr>  <int> <int>     <dbl>   <dbl>
## 1 tempohosp não    sim       88    56     1648. 0.00083

Assim como no cálculo manual, o teste no R, mostra uma diferença estatisticamente significativa (P = 0,00083) entre os tempos de hospitalização dos recém-nascidos que realizaram cirurgia no período neonatal que se infectaram ou não (diferença mediana = 14 dias; IC95% : 5,0 – 19,5).

17.4.5 Tamanho do efeito

É interessante calcular o tamanho do efeito, a magnitude do efeito. O tamanho do efeito r é calculado como a estatística \(Z_{U}\) dividida pela raiz quadrada do tamanho da amostra (\(n = n_{1} + n_{2}\)).

\[ r = \frac {Z_{U}}{\sqrt{n}} \]

O valor de \(Z_{U}\) é igual a 3.3398648, logo

r <- Z_U/sqrt(n1+n2)
round(r,3)

## [1] 0.278

O R possui a função wilcox_effsize() do pacote rstatix e necessita também do pacote coin (147) , instalado para calcular a estatística r.⁵⁸ A saída exibirá junto a magnitude o efeito, que no caso é pequena (veja Tabela 17.3).

wilcox_effsize(cirurgia, tempohosp~infec)

## # A tibble: 1 × 7
##   .y.       group1 group2 effsize    n1    n2 magnitude
## * <chr>     <chr>  <chr>    <dbl> <int> <int> <ord>    
## 1 tempohosp não    sim      0.279    88    56 small

Tabela17.3: Tabela17.4: Interpretação do valor r (sem considerar o sinal)
Valor r	Magnitude
0,10 < 0,30	pequeno
0,30 < 0,50	médio
>= 0,50	grande

17.4.6 Conclusão

O valor \(P<0,0001\), bem abaixo do nível de significância estabelecido (\(\alpha = 0,05)\). Pode-se concluir que o tempo de hospitalização nos dois grupos é estatisticamente diferente. Entretanto, a magnitude dessa diferença é pequena.

Isto pode ser visualizado no gráfico (Figura 17.2):

ggpubr::ggboxplot(cirurgia,
                   x = "infec",
                   y = "tempohosp",
                   bxp.errorbar = TRUE,
                   bxp.errorbar.width = 0.1,
                   fill = "infec",
                   palette = "nejm",
                   legend = "none",
                   ggtheme = theme_bw(),
                   xlab = "Presença de infecção" ,
                   ylab = "Tempo de hospitalização (dias)") +
  labs(subtitle = rstatix::get_test_label(teste, detailed = TRUE))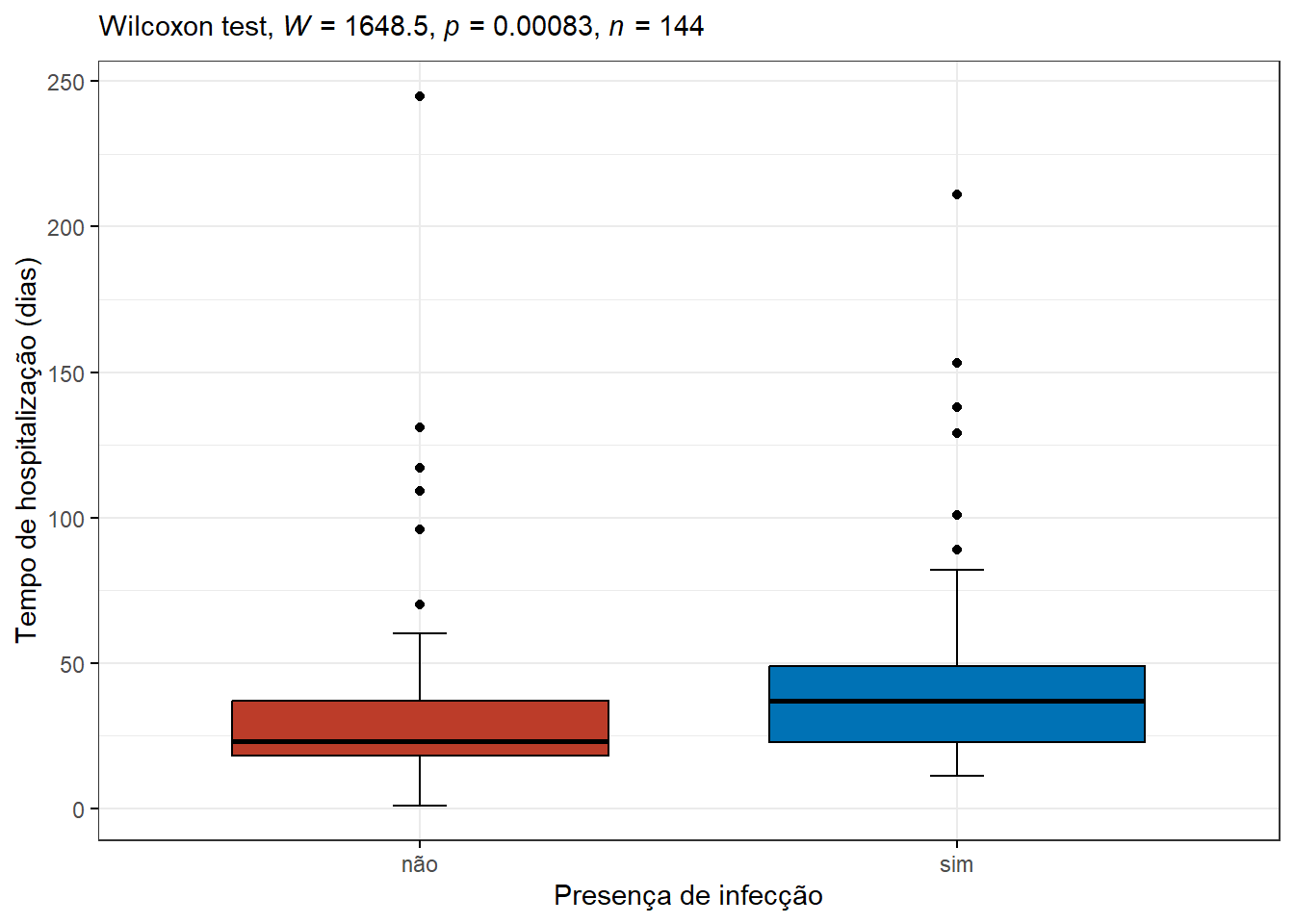

Figura17.2: Impacto da infecção no tempo de hopsitalização.

17.5 Teste de Wilcoxon

O teste de Wilcoxon, também conhecido como teste dos postos com sinais de Wilcoxon (Wilcoxon Signed-Rank Test), é um teste não paramétrico utilizado em situações em que existem dois conjuntos de dados emparelhados, ou seja, dados provenientes do mesmo participante. O teste não examina os dois grupos individualmente; em vez disso, ele se concentra na diferença existente entre cada par de observações. É um equivalente não paramétrico do teste t pareado.

17.5.1 Dados usados nesta seção

Pata verificar se a realização de exercícios aeróbicos modifica a função respiratória de 10 escolares asmáticos, foi medido o Pico de Fluxo Expiratório Máximo (Peak Flow Meter) no início e no final do programa, após 120 dias. O Pico de Fluxo Expiratório Máximo (PFE) serve como uma forma simples de avaliar a força e a velocidade de saída do ar de dentro dos pulmões. É medido em L/min. Os resultados do estudo tem apenas três variáveis, id, basal e final.

id <- c(1:10)
basal <- c(120, 200, 140, 200, 110, 240, 150, 120, 250, 190)
final <- c(220, 300, 230, 180, 300, 330, 230, 250, 300, 200)

dados <- tibble(id, basal, final)

head (dados)

## # A tibble: 6 × 3
##      id basal final
##   <int> <dbl> <dbl>
## 1     1   120   220
## 2     2   200   300
## 3     3   140   230
## 4     4   200   180
## 5     5   110   300
## 6     6   240   330

A questão de pesquisa a ser respondida, portanto, é:

Existe diferença entre as medidas iniciais e finais do PFE dos escolares asmáticos que entraram em um programa de exercícios aeróbicos?

17.5.1.1 Exploração e transformação dos dados

Os dados estão no formato amplo com as variáveis basal e final classificadas como númericas. Será transformado para o formato longo, usando a função pivot_longer() do pacote tidyr. Este processo é opcional, mas, como foi feito com o teste t pareado, será repetido aqui como treinamento:

dadosL <- dados %>% 
  tidyr::pivot_longer(c(basal, final), 
                      names_to = "momento", 
                      values_to = "medidas")
str(dadosL)

## tibble [20 × 3] (S3: tbl_df/tbl/data.frame)
##  $ id     : int [1:20] 1 1 2 2 3 3 4 4 5 5 ...
##  $ momento: chr [1:20] "basal" "final" "basal" "final" ...
##  $ medidas: num [1:20] 120 220 200 300 140 230 200 180 110 300 ...

17.5.1.2 Medidas resumidoras

Como o número de participantes é de apenas 10, a medida de posição mais adequada para resumir os dados é mediana e a medida de dispersão é o intervalo interquartil (IIQ). Para isso, se fará uso das funções group_by() e summarise() do pacote dplyr:

resumo <- dadosL %>% 
  dplyr::group_by(momento) %>% 
  dplyr::summarise(n = n(),
                   mediana = median (medidas, na.rm = TRUE),
                   p25=quantile(medidas, probs = 0.25, na.rm = TRUE),
                   p75=quantile(medidas, probs = 0.75, na.rm = TRUE),
                   media = mean (medidas, na.rm = TRUE),
                   dp = sd (medidas, na.rm = TRUE),
                   ep = dp/sqrt(n),
                   me = ep * qt(1 - (0.05/2), n - 1))
resumo

## # A tibble: 2 × 9
##   momento     n mediana   p25   p75 media    dp    ep    me
##   <chr>   <int>   <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 basal      10     170  125    200   172  50.9  16.1  36.4
## 2 final      10     240  222.   300   254  50.4  15.9  36.0

17.5.1.3 Visualização dos dados

Pode-se fazer visualização gráfica dos dados usando um boxplot (Figura 17.3 ou um gráfico de linha (Figura 17.4).

Boxplot

ggpubr::ggboxplot(dadosL,
                  x = "momento",
                  y = "medidas",
                  bxp.errorbar = TRUE,
                  bxp.errorbar.width = 0.1,
                  fill = "momento",
                  palette = c("cyan4", "cyan3"),
                  legend = "none",
                  ggtheme = theme_bw(),
                  xlab = "Momento" ,
                  ylab = "PEF (L/min) ")+
  theme (text = element_text (size = 13),
         axis.text.x= element_text(size = 12))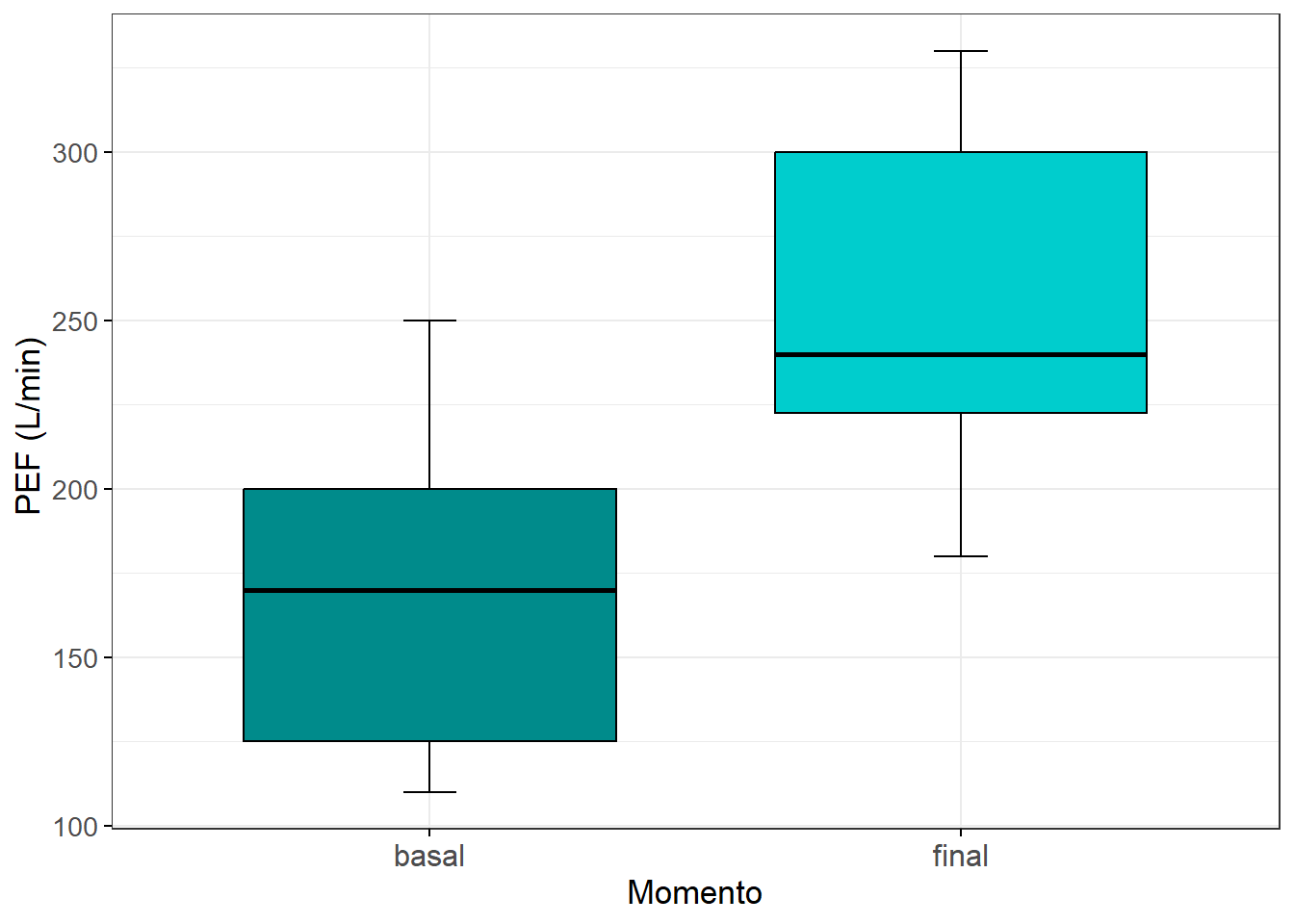

Figura17.3: Impacto de exercícios aeróbicos na função respiratória de 10 escolares asmáticos.

Gráfico de linha

ggpubr::ggline(dadosL,
               x = "momento",
               y = "medidas",
               color = "cyan4",
               linetype = "dashed",
               size = 0.7,
               add = "mean_ci",
               point.size = 2,
               xlab = "Momento" ,
               ylab = "PEF (L/min) ",
               ggtheme = theme_bw()) +
  theme (text = element_text (size = 13),
         axis.text.x= element_text(size = 12))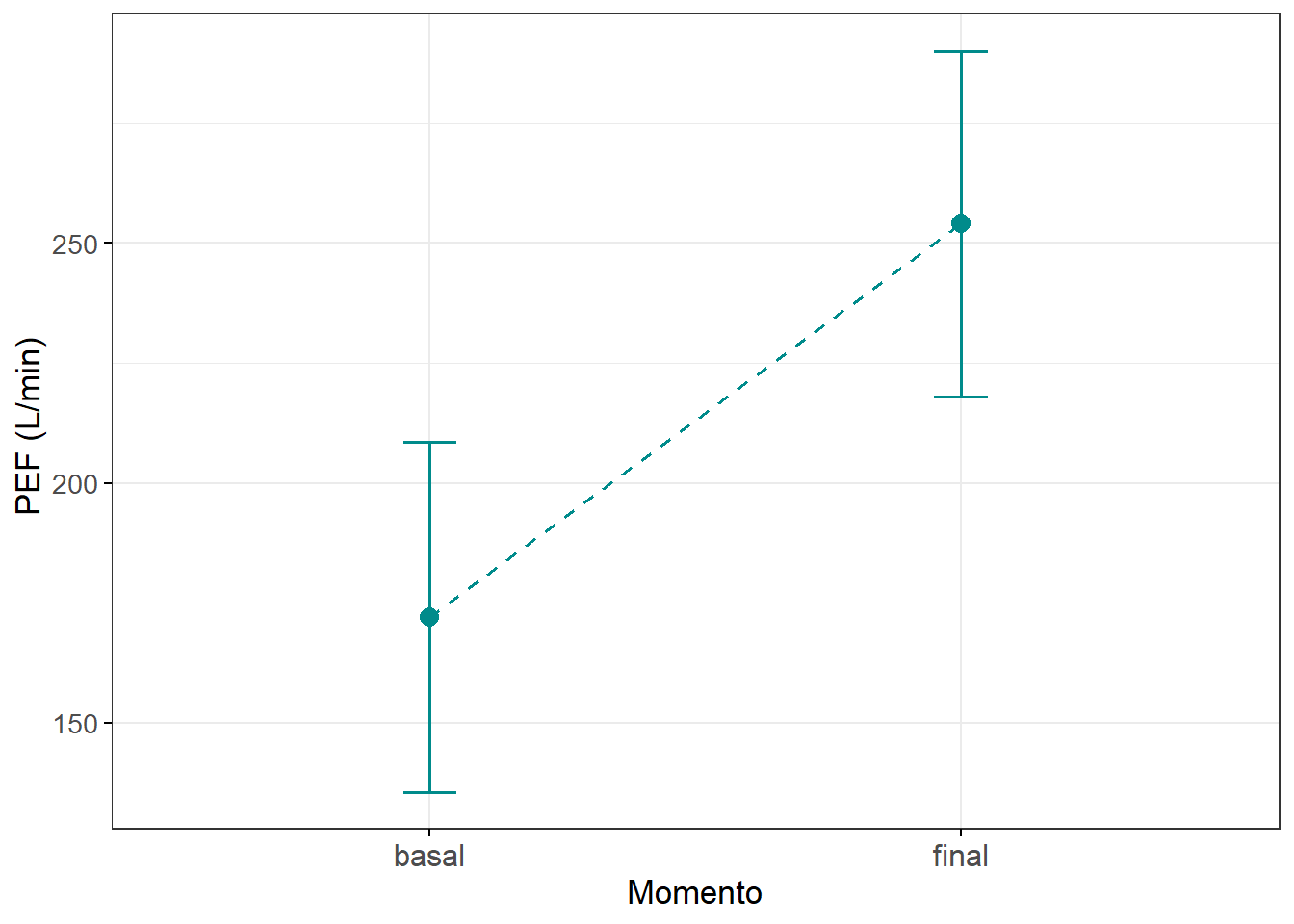

Figura17.4: Impacto de exercícios aeróbicos na função respiratória de 10 escolares asmáticos.

17.5.1.4 Criação de uma variável que represente a diferença entre os momentos

A diferença entre as média basal e final será atribuída ao nome D. Esta ação será realizada, utilizando o banco de dados amplo (dados):

dados$D <- dados$basal - dados$final
head (dados)

## # A tibble: 6 × 4
##      id basal final     D
##   <int> <dbl> <dbl> <dbl>
## 1     1   120   220  -100
## 2     2   200   300  -100
## 3     3   140   230   -90
## 4     4   200   180    20
## 5     5   110   300  -190
## 6     6   240   330   -90

Resumo da variável D

Ao resumo será atribuído ao nome resumo2:

resumo2 <- dados %>% 
  dplyr::summarise(n = n (),
                   mediana = median (D, na.rm = TRUE),
                   p25=quantile(D, probs = 0.25, na.rm = TRUE),
                   p75=quantile(D, probs = 0.75, na.rm = TRUE))
resumo2

## # A tibble: 1 × 4
##       n mediana   p25   p75
##   <int>   <dbl> <dbl> <dbl>
## 1    10     -90  -100 -57.5

O sinal negativo demonstra que houve um aumento do PFM do momento basal para o final.

17.5.2 Definição das hipóteses estatísticas

Da mesma maneira que o teste t pareado, as hipóteses estabelecidas comparam dois grupos dependentes. O teste de Wilcoxon é usado para avaliar a hipótese nula de que a distribuição das diferenças entre os grupos tem uma diferença mediana igual a 0.

\(H_{0}\): \(D_{i} = 0\) .
\(H_{A}\): \(D_{i} \ne 0\).

Note que a \(H_{A}\) estabelece que a diferença pode aumentar ou diminuir. Logo, o teste é bicaudal.

17.5.3 Execução do teste estatístico

17.5.3.1 Lógica do teste de Wilcoxon

A ideia do teste é verificar se as diferenças positivas são maiores ou menores, em grandeza absoluta, que as diferenças negativas. Para isso, foi criada, anteriormente, a variável D. Agora, será criada outra variável, iguala a variável D, apenas ignorando o sinal, denominada D_abs, diferença absoluta entre as variáveis final e basal.

dados$D_abs <- abs(dados$basal - dados$final)

Excluir os casos com diferença igual a 0 (zero). Para isso, uma maneira possível é extrair um subconjunto de dados do conjunto principal (dados), criando um conjunto de dados com a função filter() do pacote dplyr, que receberá o nome de dados1. O argumento D_absbs != 0 significa todas as diferenças absolutas diferentes de 0:

dados1 <- dados %>% dplyr::filter(D_abs != 0)

Observe que como não há diferenças zeradas. Ou seja, o novo conjunto de dados continua o mesmo. O que pode ser confirmado, executando a função str():

str (dados1)

## tibble [10 × 5] (S3: tbl_df/tbl/data.frame)
##  $ id   : int [1:10] 1 2 3 4 5 6 7 8 9 10
##  $ basal: num [1:10] 120 200 140 200 110 240 150 120 250 190
##  $ final: num [1:10] 220 300 230 180 300 330 230 250 300 200
##  $ D    : num [1:10] -100 -100 -90 20 -190 -90 -80 -130 -50 -10
##  $ D_abs: num [1:10] 100 100 90 20 190 90 80 130 50 10

Ordenar de forma crescente todos os valores da variável D_abs do banco de dados dados1, usando a função arrange() do pacote dplyr:

dados1 <- dados1 %>% dplyr::arrange(dados1$D_abs)

Estabelecer postos para os valores ordenados da variável D_abs, do conjunto de dados dados1, fazendo a média das ordens quando houver empate. A execução deste comando cria uma nova variável, chamada postos:

dados1$postos <- rank(dados1$D_abs)

Estabelecer sinais para os postos, criando dois subconjuntos de dados do conjuntos dados1, um com os escolares com postos positivos (pos) e outros com postos negativos(neg):

neg <- dados1 %>% dplyr::filter(D < 0)
pos <- dados1 %>% dplyr::filter(D > 0)

Somar todos os postos (variável posto) em cada um dos subconjuntos criados (neg e pos):

soma_neg <- sum(neg$postos)
soma_pos <- sum(pos$postos)
print (c(soma_neg, soma_pos))

## [1] 53  2

Atribuir a menor soma à estatística do teste, denotada T:

T <- min (soma_neg : soma_pos)
T

## [1] 2

Para dados com tamanhos grandes (> 20 pares), a significância de T pode ser determinada (148), considerando que a distribuição de T tem aproximadamente distribuição normal com média igual a

\[ \mu_{T} =\frac{n \times \left (n + 1 \right )}{4} \]

onde n é o tamanho da amostra.

n <- length(dados$D)
mu_T <- (n * (n + 1))/4
mu_T

## [1] 27.5

E desvio padrão igual a:

\[ \sigma_{T}= \sqrt {\frac{n\left (n + 1 \right )\times \left (2n + 1 \right )}{24}} \]

dp_T <- sqrt ((n*(n + 1)) * (2 * n + 1) /24) 
dp_T

## [1] 9.810708

Os resultados da execução das equações fornecem os dados para calcular a estatística Z_T com correção de continuidade e, a partir dela, calcular o valor P.

\[ Z_{T}= \frac{\left |T - \mu_{T} \right | - 0,5}{\sigma_{T}} \]

Z_T <- (abs(T - mu_T)- 0.5)/dp_T
Z_T

## [1] 2.548236

Concluindo, o valor da estatística de teste T é superior ao \(Z_{crítico} = 1,96\), para um \(\alpha = 0,05\). Dessa forma, a \(H_{0}\) é rejeitada. Existe uma diferença significativa entre o PFE basal e o PFE final, neste grupo de escolares asmáticos.
O valor P pode ser obtido com a função pnorm() e multiplicando o resultado por 2, pois o teste é bilateral.

P <- pnorm (Z_T, lower.tail = FALSE) * 2
P

## [1] 0.01082692

Como já dito anteriormente, na prática, não há necessidade de fazer todos esses cálculos, pois o R calcula facilmente o teste. Eles são apenas uma demonstração de como o teste funciona.

17.5.3.2 Cálculo do teste de Wilcoxon no R

Usando o conjunto de dados no formato longo (dadosL), calcula-se o teste com a função wilcox_test() do pacote rstatix. É a mesma função utilizada para o teste de U de Mann-Whitney, mudando apenas o argumento paired=FALSE para paired=TRUE:

teste1 <- dadosL %>% 
  rstatix::wilcox_test(medidas ~ momento, paired = TRUE) %>% 
  rstatix::add_significance()
teste1

## # A tibble: 1 × 8
##   .y.     group1 group2    n1    n2 statistic      p p.signif
##   <chr>   <chr>  <chr>  <int> <int>     <dbl>  <dbl> <chr>   
## 1 medidas basal  final     10    10         2 0.0107 *

Observe que o resultado é o mesmo calculado manualmente.

17.5.4 Tamanho do efeito

O tamanho do efeito pode ser calculado da mesma forma que para o teste de Mann-Whitney (Seção 17.4.5), usando a mesma equação e os dados obtidos acima, onde 2.548236 e n = 10 tem-se

\[ r = \frac {Z_{T}}{\sqrt{n}} \]

Pode-se usar também a função wilcox_effsize() para calcular a estatística r. A Saída exibe junto a magnitude o efeito, que no caso é grande (> 0,5 como mostra a Tabela 17.3 do teste de Mann-Whitney).

dadosL %>% 
  wilcox_effsize(medidas ~ momento, paired = TRUE)

## # A tibble: 1 × 7
##   .y.     group1 group2 effsize    n1    n2 magnitude
## * <chr>   <chr>  <chr>    <dbl> <int> <int> <ord>    
## 1 medidas basal  final    0.823    10    10 large

17.5.5 Conclusão

Assumindo um \(\alpha = 0,05\), se o valor P, obtido pelo teste, for menor do que 0,05, rejeita-se a hipótese nula (V = 2, P = 0,01, n = 10).

Pode-se concluir que existe diferença nas medidas do pico de fluxo expiratório máximo no início e no fim do programa de exercícios aeróbicos realizados pelos escolares asmáticos e a magnitude do efeito foi grande (r = 0,82).

Isto pode ser visualizado na Figura 17.5:

bxp <- ggpubr::ggboxplot(dadosL,
                         x = "momento",
                         y = "medidas",
                         bxp.errorbar = TRUE,
                         bxp.errorbar.width = 0.1,
                         fill = "momento",
                         palette = c("cyan4", "cyan3"),
                         legend = "none",
                         ggtheme = theme_bw(),
                         xlab = "Momento" ,
                         ylab = "PEF (L/min) ") +
  theme (text = element_text (size = 13),
         axis.text.x = element_text(size = 11))

teste <- dadosL %>% 
  rstatix::wilcox_test (medidas ~ momento, paired = TRUE) %>%
  rstatix::add_significance ()
teste <- teste %>% rstatix::add_xy_position ()

bxp + 
  stat_pvalue_manual (teste, 
                      tip.length = 0) +
  labs (subtitle = get_test_label (stat.test = teste, 
                                   detailed = TRUE))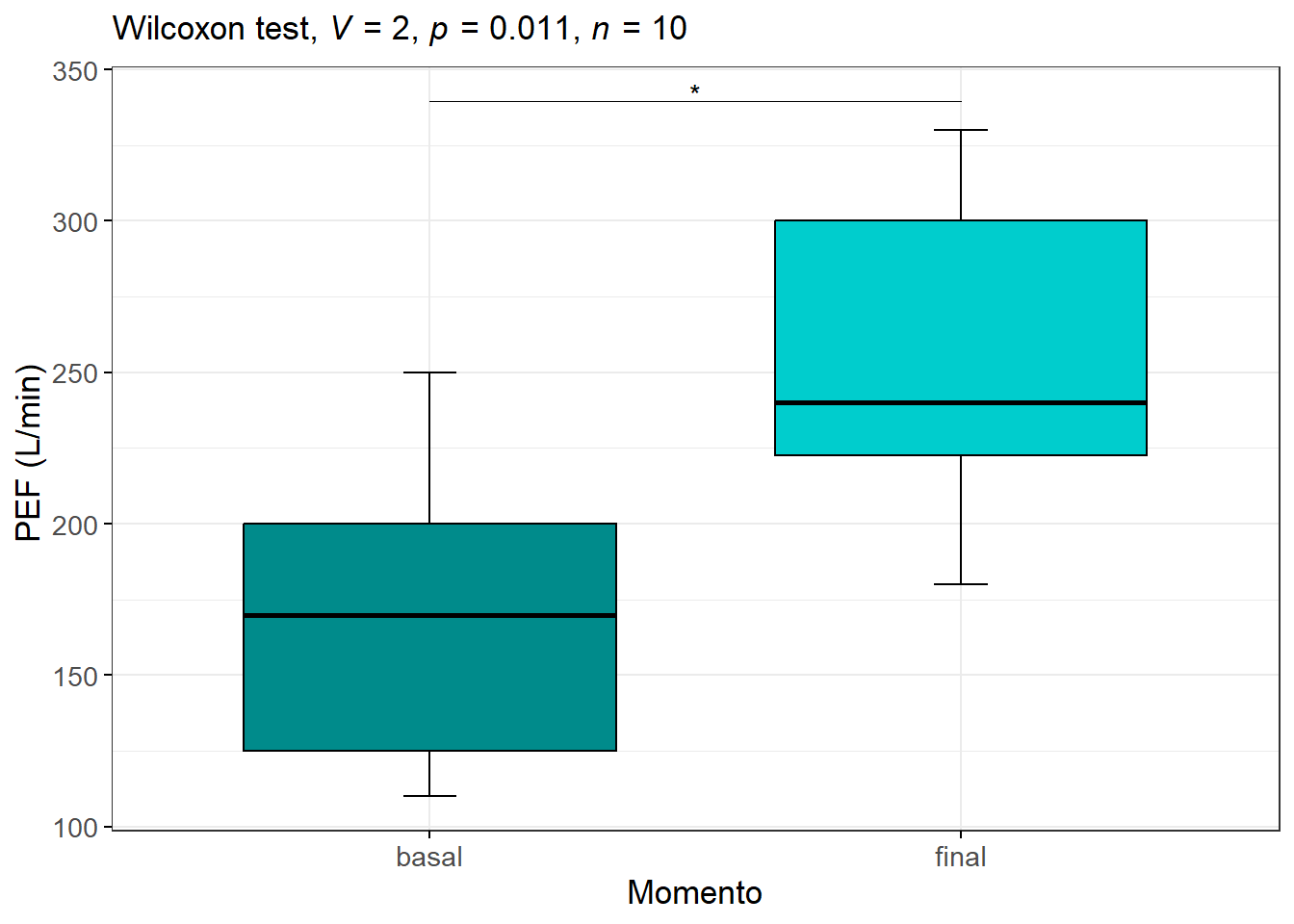

Figura17.5: Impacto de exercícios aeróbicos na função respiratória de 10 escolares asmáticos.

17.6 Teste de Kruskal-Wallis

Quando os pressupostos subjacentes a ANOVA não são atendidos, é possível usar o teste não paramétrico de Kruskal-Wallis (KW) para testar a hipótese de que os parâmetros de localização são iguais. Pode ser considerado uma extensão do teste de Wilcoxon-Mann-Whitney.

Enquanto a ANOVA depende da hipótese de que todas as populações são independentes e normalmente distribuídas, o teste de Kruskal-Wallis exige apenas amostras aleatórias independentes provenientes de suas respectivas populações. Entretanto, este teste somente deve ser aplicado se a amostra for pequena e/ou os pressupostos para a ANOVA forem seriamente violados.

O teste não usa diretamente medições de quantidade conhecida, utiliza, como outros testes não paramétricos, os postos dos valores analisados. Em função disso, é também conhecido como análise de variância de um fator em postos.

17.6.1 Dados usados nesta seção

Um experimento foi realizado para verificar se o álcool ou o café afetam os tempos de reação ao dirigir (149). O estudo tem três grupos diferentes de participantes: 10 bebendo água (controle), 10 bebendo cerveja contendo duas unidades de álcool e 10 bebendo café. O tempo de reação em uma simulação de direção foi medido para cada participante.

Os dados encontram-se no arquivo dadosResposta.xlsx. Clique aqui para baixar e, após, salve o mesmo no seu diretório de trabalho.

As variáveis são:

id \(\to\) identificação do participante;
tempo \(\to\) tempo de reação na simulação de direção em segundos;
bebida \(\to\) três grupo: água, álcool e café.

O estudo pretende verificar se existe diferença no tempo de reação dos participantes em um teste de direção com a ingesta de água, café e álcool.

17.6.1.1 Leitura e exploração dos dados

Como o dados estão contidos em um arquivo Excel (.xlsx), serão lidos com a função read_excel() do pacote readxl e a sua estrutura será observada com função str():

dados <- read_excel ("Arquivos/dadosResposta.xlsx")
str(dados)

## tibble [30 × 3] (S3: tbl_df/tbl/data.frame)
##  $ id    : num [1:30] 1 2 3 4 5 6 7 8 9 10 ...
##  $ tempo : num [1:30] 0.37 0.38 0.61 0.78 0.83 0.86 0.9 0.95 1.63 1.97 ...
##  $ bebida: chr [1:30] "agua" "agua" "agua" "agua" ...

O formato do arquivo é o longo. A variável bebida encontra-se como caracter e deve ser transformada em fator e as categorias na sequência: agua, cafe e alcool.

dados$bebida <- factor(dados$bebida, 
                       levels = c("agua", "cafe", "alcool"))

Os dados serão observados visualmente através de boxplots (Figura 17.6), usando a função ggplot() do pacote ggplot2, com cores do nejm (New England Journal of Medicine) o pacote ggsci.

ggpubr::ggboxplot(dados,
                   x = "bebida",
                   y = "tempo",
                   bxp.errorbar = T,
                   bxp.errorbar.width = 0.1,
                   fill = "bebida",
                   palette = "nejm",
                   legend = "none",
                   ggtheme = theme_bw(),
                   xlab = "Tipo de bebida" ,
                   ylab = "Tempo de reação (seg)") +
  theme(text = element_text(size = 12))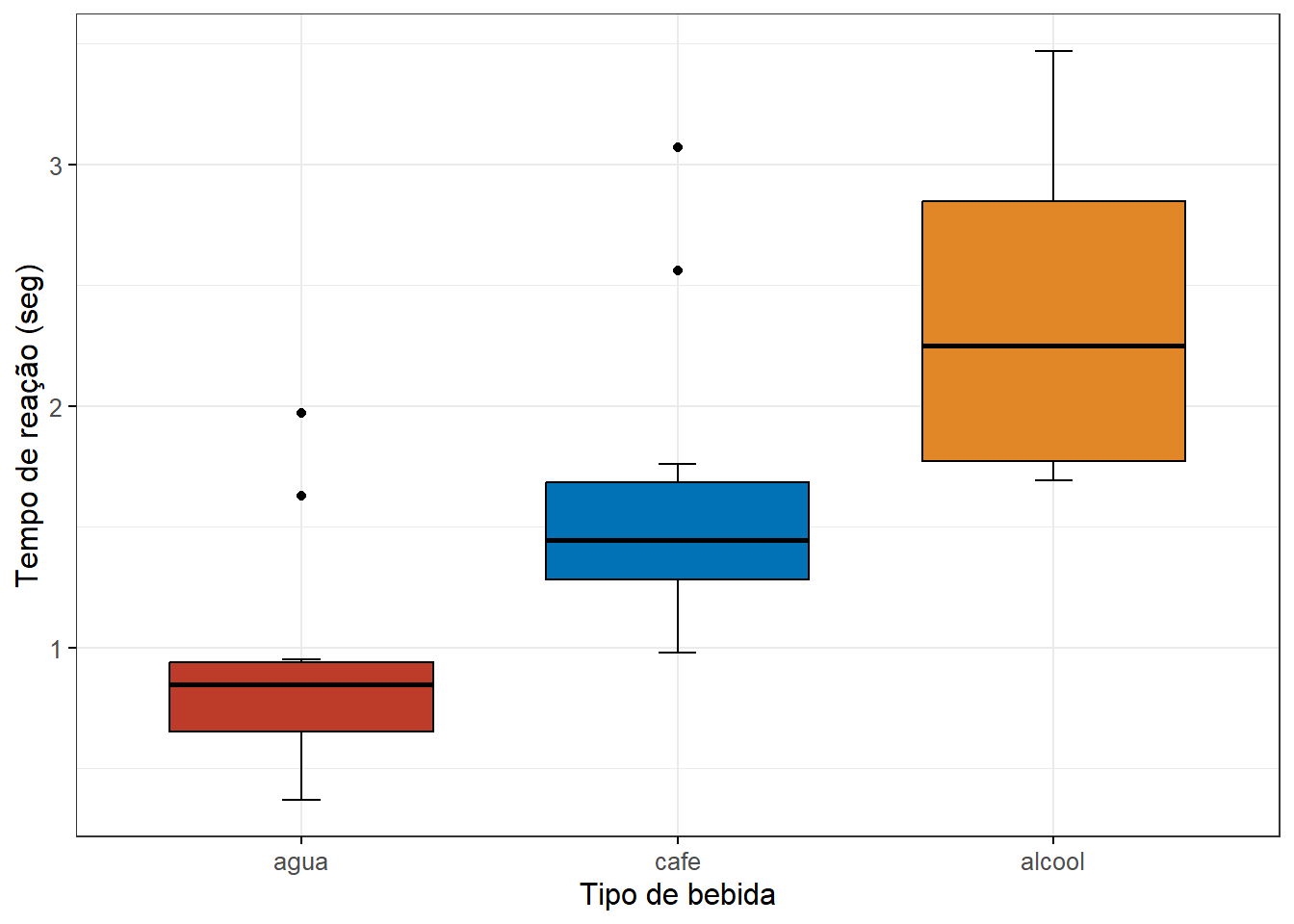

Figura17.6: Impacto do tipo de bebida no tempo de reação ao dirigir.

Os boxplots exibem dados com medianas visualmente diferentes, bigodes diferentes e grupos com presença de outliers. Para verificar o impacto desses achados, pode-se usar a função identify_outliers(), do pacote rstatix que confirma na sua Saída a presença de outliers no grupo agua e cafe, sendo dois extremos.

dados %>% 
  dplyr::group_by(bebida) %>% 
  rstatix::identify_outliers(tempo)

## # A tibble: 4 × 5
##   bebida    id tempo is.outlier is.extreme
##   <fct>  <dbl> <dbl> <lgl>      <lgl>     
## 1 agua       9  1.63 TRUE       FALSE     
## 2 agua      10  1.97 TRUE       TRUE      
## 3 cafe      19  2.56 TRUE       FALSE     
## 4 cafe      20  3.07 TRUE       TRUE

Para avaliar a normalidade será usado o teste de Shapiro-Wilk, com a função shapiro_test() e a função group_by() do pacote dplyr:

dados %>% 
  dplyr::group_by (bebida) %>% 
  rstatix::shapiro_test (tempo)

## # A tibble: 3 × 4
##   bebida variable statistic      p
##   <fct>  <chr>        <dbl>  <dbl>
## 1 agua   tempo        0.863 0.0837
## 2 cafe   tempo        0.815 0.0220
## 3 alcool tempo        0.875 0.114

A variável cafe tem uma distribuição que não se ajusta a distribuição normal.

Para completar a exploração dos dados, será solicitado, usando as funções group_by () e summarise, do pacote dplyr, medidas de localização e dispersão adquadas para variáveis bem assimétricas.

resumo <- dados %>% 
  dplyr::group_by(bebida) %>% 
  dplyr::summarise(n = n(),
                   mediana = median (tempo, na.rm = TRUE),
                   p25=quantile(tempo, probs = 0.25, na.rm = TRUE),
                   p75=quantile(tempo, probs = 0.75, na.rm = TRUE))
resumo

## # A tibble: 3 × 5
##   bebida     n mediana   p25   p75
##   <fct>  <int>   <dbl> <dbl> <dbl>
## 1 agua      10   0.845 0.653 0.937
## 2 cafe      10   1.44  1.28  1.68 
## 3 alcool    10   2.25  1.77  2.85

17.6.2 Hipóteses estatísticas

Se não houver diferença entre os grupos, ou seja, os grupos são provenientes de uma mesma população, as somas dos postos em cada grupo devem ficar próximas. Desta forma,

\(H_{0}\): As populações são iguais.
\(H_{1}\): Pelo menos uma das populações tende a exibir valores diferentes do que as outras populações.

17.6.3 Pressupostos do teste

O teste de Kruskal-Wallis pressupõe as seguintes condições para o seu adequado uso:

As amostras são amostras aleatórias independentes de suas respectivas populações;
A escala de medição utilizada é pelo menos ordinal e, se houver apenas três grupos, deve haver pelo menos 5 casos em cada grupo;
As distribuições dos valores nas populações amostradas são idênticas, exceto pela possibilidade de que uma ou mais das populações sejam compostas por valores que tendem a ser maiores do que os das outras populações.

17.6.4 Execução do teste estatístico

17.6.4.1 Lógica do teste de Kruskall-Wallis

A teoria do teste Kruskal-Wallis é semelhante à do teste de Mann-Whitney, ou seja, tem como base a soma dos postos. Em primeiro lugar, os escores são ordenados do menor para o maior, independentemente do grupo que pertençam.

O menor recebe o posto 1 e assim por diante. Após a atribuição dos postos, soma-se os postos por grupo. A soma dos postos de cada grupo é representada por \(R_{1}\), \(R_{2}\), \(R_{3}\), …, \(R_{i}\). A estatística do teste, H, é calculada com a equação (150):

\[ H =\frac {12}{N \times \left (N + 1 \right )} \sum_{i=1}^{k} \frac {R_{i}^{2}}{n_{{i}}}-3 \times\left (N + 1\right) \]

onde \(n_{i}\) é o número de observações no grupo i, \(N = \sum_{i=1}^{k}\times n_{i}\) (o número total de observações em todos os k grupos) e \(R_{i}\) é a soma dos postos das \(n_{i}\) observações no grupo i.

Uma boa verificação (mas não uma garantia) de que os postos foram atribuídos corretamente é ver se a soma de todos os postos é igual a \(\frac {N \times \left (N + 1\right )}{2}\).

Criar a variável posto com os postos ordenados de forma crescente, independente do grupo, como realizado no teste de Mann-Whitney:

dados$posto <- rank(dados$tempo, ties.method = "average")
str(dados)

## tibble [30 × 4] (S3: tbl_df/tbl/data.frame)
##  $ id    : num [1:30] 1 2 3 4 5 6 7 8 9 10 ...
##  $ tempo : num [1:30] 0.37 0.38 0.61 0.78 0.83 0.86 0.9 0.95 1.63 1.97 ...
##  $ bebida: Factor w/ 3 levels "agua","cafe",..: 1 1 1 1 1 1 1 1 1 1 ...
##  $ posto : num [1:30] 1 2 3 4 5 6 7 8 16 22.5 ...

Somar os postos de cada grupo separadamente:

resumo1 <- dados %>% 
  dplyr::group_by(bebida) %>% 
  dplyr::summarise(n = n(),
                   soma = sum(posto))
resumo1

## # A tibble: 3 × 3
##   bebida     n  soma
##   <fct>  <int> <dbl>
## 1 agua      10  74.5
## 2 cafe      10 157  
## 3 alcool    10 234.

Cálculo da estatística do teste H

N <- 30
n <- 10
R_agua <- resumo1[1,3]
R_alcool <- resumo1[2,3]
R_cafe <- resumo1[3,3]

H <- (12/(N*(N+1))) * ((R_agua^2/n) + (R_alcool^2/n) + (R_cafe^2/n)) - (3*(N+1))
H

##       soma
## 1 16.31806

Cálculo do Valor P

Se existir três grupos, com cinco ou menos participantes em cada grupo, há necessidade de usar a tabela especial para tamanhos de amostra pequenos (151). Se você tiver mais de cinco participantes por grupo, trate H como qui-quadrado. A estatística H é estatisticamente significativo se for igual ou maior que o valor crítico qui-quadrado para o grau de liberdade específico, igual a \(k - 1\). Aqui, tem-se 10 participantes por grupo e, assumindo um \(\alpha = 0,05\), o \(H_{crítico}\) é igual a:

alpha <- 0.05
k <- 3
gl = k - 1
H_critico <- qchisq(1 - alpha, gl)
H_critico

## [1] 5.991465

Uma vez que o \(H_{calculado} = 16,3\) é maior que \(H_{crítico} = 6,0\) , rejeita-se a \(H_{0}\). O valor Pé obtido através da função pchisq():

H <- 16.32
pchisq(H, 2, lower.tail = FALSE)

## [1] 0.0002858624

O R tem funções que fazem facilmente esses cálculos enfadonhos. Eles são colocados aqui apenas para ilustrar o raciocínio de como o teste de Kruskal-Wallis funciona. Sempre existem curiosos lendo o livro!

17.6.4.2 Teste de Kruskal-Wallis no R

No R, pode-se calcular o teste, usando a função kruskal_test() do pacote rstatix, cujos argumentos podem ser consultados na ajuda do RStudio.

teste <- rstatix::kruskal_test (data = dados, formula = tempo ~ bebida)
teste

## # A tibble: 1 × 6
##   .y.       n statistic    df        p method        
## * <chr> <int>     <dbl> <int>    <dbl> <chr>         
## 1 tempo    30      16.3     2 0.000286 Kruskal-Wallis

17.6.5 Tamanho do efeito

O eta quadrado (\(\eta^{2}\)), com base na estatística H, pode ser usado como a medida do tamanho do efeito do teste de Kruskal-Wallis. É calculado pela equação:

\[ \eta_{H}^{2} = \frac {\left (H - k + 1 \right)}{\left (N - k\right)} \]

onde H é a estatística obtida no teste de Kruskal-Wallis; k é o número de grupos; N é o número total de observações (152).

A estimativa eta ao quadrado assume valores de 0 a 1 e, multiplicada por 100, indica a porcentagem de variância na variável dependente explicada pela variável independente. Pode ser obtido no R com a função kruskal_effsize() do pacote rstatix:

dados %>% kruskal_effsize (tempo~bebida)

## # A tibble: 1 × 5
##   .y.       n effsize method  magnitude
## * <chr> <int>   <dbl> <chr>   <ord>    
## 1 tempo    30   0.530 eta2[H] large

Um efeito \(\ge 0,14\) é considerado grande e \(<0,06\) é pequeno (117).

17.6.6 Testes post hoc

A partir do resultado do teste de Kruskal-Wallis, sabe-se que há uma diferença significativa entre os grupos, mas não se sabe quais pares de grupos são diferentes.

Um teste de Kruskal-Wallis significativo é geralmente seguido pelo teste de Dunn (153) para identificar quais grupos são diferentes.

Para realizar as múltiplas comparações, no R, pode ser usada a função dunn_test(), incluído no pacote rstatix. O ajuste de P é feito pelo método de Bonferroni:

pwc <- dados %>% 
  dunn_test (tempo ~ bebida, p.adjust.method = "bonferroni") 
pwc

## # A tibble: 3 × 9
##   .y.   group1 group2    n1    n2 statistic         p    p.adj p.adj.signif
## * <chr> <chr>  <chr>  <int> <int>     <dbl>     <dbl>    <dbl> <chr>       
## 1 tempo agua   cafe      10    10      2.10 0.0361    0.108    ns          
## 2 tempo agua   alcool    10    10      4.04 0.0000537 0.000161 ***         
## 3 tempo cafe   alcool    10    10      1.94 0.0520    0.156    ns

A saída do teste de Dunn, mostra que existe uma diferença estatisticamente significativa apenas entre a água e o álcool.

17.6.7 Conclusão

Um teste de Kruskal-Wallis foi realizado para comparar os tempos de reação em uma simulação de direção após beber água, café ou álcool. Houve evidência de uma diferença (P = 0,00029) de pelo menos um par de grupos (Figura 17.7).

O teste de comparações de pares, usando o teste de Dunn, foi realizado para os três pares de grupos. Houve evidencia de diferença entre o grupo que consumiu duas unidades de álcool e o grupo que ingeriu água (P ajustado (Bonferroni) = 0,00016). Entre os demais pares não houve diferença significativa. O tempo mediano de reação para o grupo que recebeu água foi de 0,84 (0,65 – 0,94) segundos, em comparação com 2,25(1,77 – 2,85) segundos no grupo que bebeu cerveja equivalente a duas unidades de álcool, enquanto para o café foi de 1,45(1,28 – 1,69) segundos.

pwc <- pwc %>% rstatix::add_xy_position(x= "bebida")

ggpubr::ggboxplot(dados,
                  x = "bebida",
                  y = "tempo",
                  bxp.errorbar = TRUE,
                  bxp.errorbar.width = 0.1,
                  fill = "bebida",
                  palette = "nejm",
                  legend = "none",
                  ggtheme = theme_bw())+
  ggpubr::stat_pvalue_manual (pwc,
                              label = "p = {scales::pvalue(p.adj)}",
                              label.size = 3.2,
                              hide.ns = FALSE) +
  ggplot2::labs(x = "Tipo de bebida", 
                y = "Tempo de reação (seg)",
                subtitle = get_test_label (teste, detailed = TRUE),
                caption = get_pwc_label(pwc))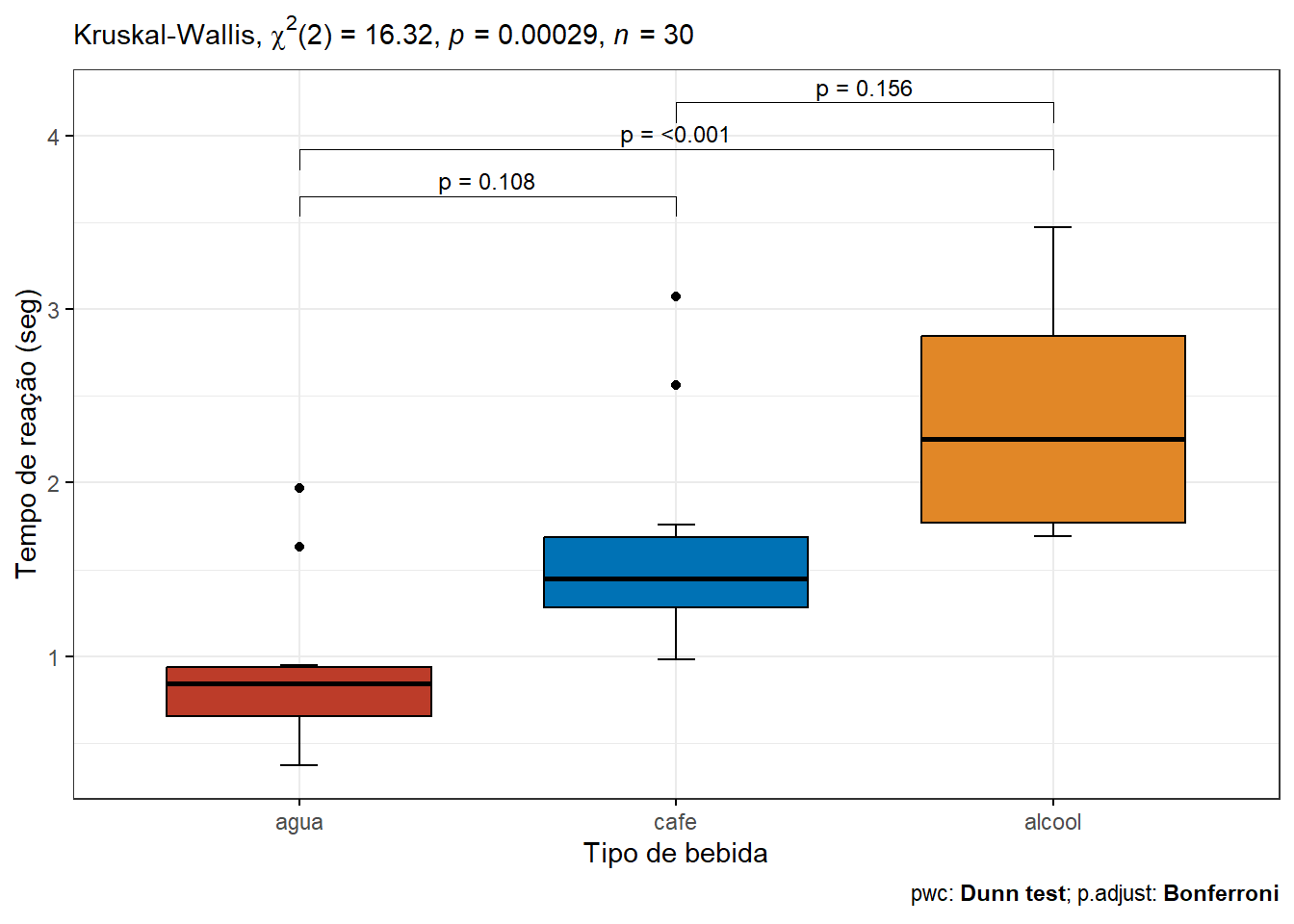

Figura17.7: Impacto do tipo de bebida no tempo de reação ao dirigir.

O cálculo pode também ser realizado, usando a função wilcox.test() do pacote stats, incluído no R base.↩︎
Para maiores detalhes consulte a ajuda da função.↩︎